RTP (RETURN TO PLAYER) - RETUR LA JUCĂTOR

“Return to Player” (RTP) sau procentajul de câștig la un joc de cazinou este definit de următoarea formulă:

Reține că acest număr se bazează pe pariuri și câștiguri reale. Nu este un număr teoretic. Nu e calculat pe baza unu calcul tabelar, prin rularea unui ciclu sau printr-o simulare extinsă a jocului. RTP este bazat pe analiza făcută unor oameni reali care au plasat pariuri pe jocuri în cazinouri reale.

Pentru jocurile care nu au strategie (precum Casino War, zaruri sau ruletă) de obicei se aplică următoarea formulă:

Mai mult, cu cât jocul este jucat mai des, cu atât mai mult RTP-ul e mai concludent: reprezintă informații despre câștigul real al jocului și un mult mai “exact” mod în care ne așteptăm că această ecuație să devină realitate. “Exact” nu înseamnă că două părți se aproprie din ce în ce mai mult. Înseamnă că media celor două aspecte ale acestei ecuații se apropie din ce în ce mai mult de 1, în timp ce numărul de runde devine din ce în ce mai mare. [100% – (House Edge)] / RTP > 1

Numărul 100% – (House Edge) se referă la RTP-ul teoretic al jocului. Câteodată limbajul se pierde aici, iar valoarea 100% – (House Edge) se referă la RTP-ul jocului.

SĂ EXEMPLIFICĂM:

Pentru ruletă, RTP este 100% - 5.26% = 94.74%

Avem în vedere un jucător de zaruri care pariază pe pass line cu no odds pentru un avantaj al casei de 1,41%. Pentru că nu există strategie la zaruri, RTP pentru un pariu pe pass line este de 100% - 1.41% = 98.59%. Pentru Jacks sau Better cu un “9/6” pay table, RTP este 100% = 0.46% = 99.54%. Cu “8/5” pay table, RTP este 100% - 2.70% = 97.30%.

Sloturile loose au un RTP de peste 96%. Sloturile tight au au RTP sub 92%. Să ne întoarcem la aceste loterii și să investigăm RTP. În orice loterie există un milion de tichete. Să presupunem că toate acestea au fost vândute. Totalul pariat de către jucători este de 1 milion de dolari. Totalul sumei câștigate de către jucători este de 900.000 de dolari: ori 900.000 de tichete pe care s-a plătit câte un dolar, ori 9 tichete pe care s-au plătit câte 100.000 de dolari.

Prin urmare, în situația în care s-a produs o tură completă, RTP este:

Să presupunem că avem și o a doua loterie și vindem 500.000 de tichete. Prin urmare, suma totala pariată este de 500.000 de dolari. Știm că exact 90% dintre tichete sunt câștigătoare. Deci, știind avantajul casei, ne așteptăm ca jucătorii să câștige aproximativ 90% din cei 5000.000 de dolari sau aproximativ 450.000 de dolari. Statul își trage partea lui de 50.000 de dolari. Pentru a doua loterie, acest venit este aproape sigur din cauza ratei ridicate de hit (frecvența de hit = 90%) și a payout-ului scăzut din tichetele câștigătoare. RTP-ul teoretic se transferă spre o curată așteptare despre ceea ce se va întâmplă cu adevărat. 

Acum, să presupunem că oferim loteria 1 și vindem 500.000 de tichete. Iarăși, suma toatala pariată este de 500.000 de dolari. Sunt doar 9 bilete câștigătoare în lotul de un milion de tichete, astfel că undeva între 0 și 9 dintre biletele câștigătoare vor fi vândute. Mai aproape de adevăr este că 4 sau 5 bilete câștigătoare vor fi vândute. Un pic mai puțin probabil este ca 3 sau 6 bilete câștigătoare să fie vândute. Și tot așa, cu un caz dintre cele mai improbabile ca ori 0 ori 9 bilete câștigătoare să fie vândute.

Bazându-ne pe un avantaj al casei de 10%, ne așteptăm ca jucătorii să câștige aproximativ 90% din 500.000 de dolari sau 450.000 de dolari. Pentru că tichetele câștigătoare valorează fiecare 100.000 de dolari și sunt doar 8 tichete câștigătoare, jucătorii de fapt vor câștiga câteva sute de mii de dolari, fără a putea stabili cota exactă, de la 0 dolari la 900.000 de dolari. Cea mai probabilă situație este aceea în care jucătorii câștigă ori 400.000 de dolari ori 500.000 de dolari (4 sau 5 tichete câștigătoare). Este pur și simplu imposibil să câștige 90% din 5000.000 de dolari (450.000 de dolari). Dacă vindem 4 bilete câștigătoare, RTP este ($400,000) / ($500,000) = 80%. Dâcă vindem 5 bilete câștigătoare, RTP este ($500,000) / ($500,000) = 100%. Nu vom avea niciodată un RTP de 90% dacă vom vinde exact 500.000 de tichete.

Acum vom avea în vedere câteva exemple reale din cazinou. Dacă jucătorul aruncă un milion de zaruri pariind pe pass line și pariază 1 dolar pe fiecare rundă, atunci, la finalul acestui milion de aruncări, jucătorul a pariat 1 milion de dolari. Teoretic, jucătorul a recâștigat ceva în jurul a 985.900 de dolari din aceste pariuri inițiale. Pentru că pierderile și câștigurile pe pariul pass line sunt oarecum echilibrate (ca în loteria 2), acesta e un pariu sigur pe care jucătorul mai degrabă câștigă sau teoretic câștigă, astfel RTP trebuie să fie undeva destul de aproape de 98,58%. Cu cât va juca mai mult, cu atât RTP va ajunge mai aproape de 98,59% pe pass line.

SSă presupune că un om joacă la ruletă și pariază 1 dolar straight up pe 7-roșu. În această situație, avantajul casei este de 5,26%. De aceea ne așteptăm ca RTP să fie aproximativ 94,74%. Dacă acest jucător pariază 1 dolar pe 7-roșu preț de un milion de rotiri ale ruletei, atunci, la finalul acestor rotiri, jucătorul a pariat un milion de dolari și, “teoretic”, a recâștigat aproximativ 947.400 de dolari. Pentru că lovirea lui 7-roșu este un eveniment care nu se întâmplă foarte des – 1 din 38 – este rezonabil să ne așteptăm să fie o diferență substanțială între succesul real și cel teoretic (la fel ca în cazul loteriei 1). Acum să presupunem că un jucător pariază același milion de dolari dar o singură dată pe “even”, iar nu pe 7-roșu. În acest caz, pentru că situația de câștig sau pierdere se întâmplă aproape la fel de des, RTP va acoperi rapid până la 94,74% pentru acest jucător.

Ideea e că RTP-ul teoretic ar trebui să fie destul de asemănător cu RTP-ul real pentru jocurile la care nu e necesară nici o strategie și au o rată ridicată de hit. Cu cât evenimentul “succes” e mai rar (cu cât e mai rară frecvența de hit), cu atât e necesar mai mult joc pentru ca aceste valori să se acopere una pe alta.

Pentru jocurile unde se poate aplica o strategie, greșelile vor fi făcute de jucători. Din această cauză, valoare RTP este, de obicei, mai mică de 100% – (House Edge). Pentru jocurile cu o strategie relativ banală (ca Three Card Poker), RTP este de obicei doar cu ceva mai puțin de 100% – (House Edge). Pentru jocurile extrem de complicate ca Blackjack Switch sau Super Fun 21, RTP-ul poate fi cu câteva puncte procentuale sub valoarea teoretică.

Multe cazinouri (în special cele online unde fiecare interacțiune a jucătorului este înregistrată) crează rapoarte lunare de RTP astfel că pot urmări performanța exactă a fiecărui joc. Figura 4 îți oferă exemple de RTP-uri pentru o lună din partea unui cazinou, raport bazat pe ce s-a jucat live. Uită-te atent la acest tabel din care putem extrage câteva observații.

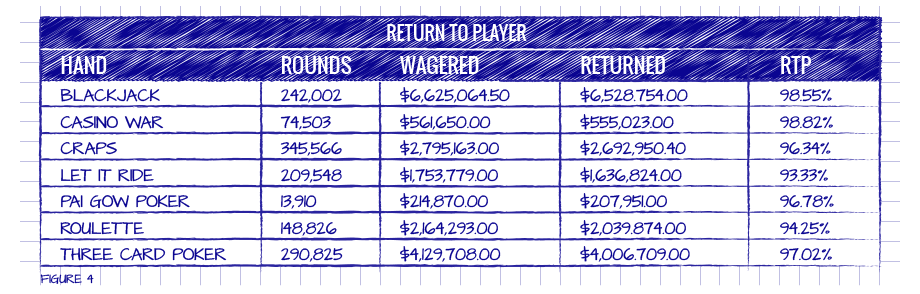
Ține seama de faptul că Let it Ride, Pai Gow și Three Card Poker întorc sub RTP-ul teoretic pentru o strategie perfectă. Având la bază rezultatele oferite de Figura 1, Blackjack-ul are un RTP teoretic de 99,54%; Let it Ride de 97,96,49%; Pai Gow Poker de 97,34%; Three Card Poker de 97,15%. Pe de altă parte, Casino War este deasupra RTP-ul teoretic de 97,10%, iar ruleta este aproape de un RTP teoretic de 94,74%. RTP-ul pentru zaruri nu poate fi analizat din cauza sumedeniei de pariuri posibile.

Fii atent la o eroare des întâlnită. Cărțile, zarurile, tamburii de sloturi și roțile de rulete nu știu ce RTP teoretic ar trebuie să aducă și de ce RTP teoretic ar trebui să se apropie. Dacă RTP pentru ruletă este de 94,25% după 148.826 de rotiri, nu e nici o așteptare ca jocul să încerce și să ajungă la același nivel după următoarele 148.826 de rotiri, astfel că RTP-ul se mișcă aproape de o valoare teoretică de 94,74%. Dacă pass line la zaruri întoarce 102%, asta nu înseamnă că zarurile se vor răci. RTP-ul real nu este o indicație a ceea ce se va întâmpla în viitor încât să facă diferența. Sau, așa cum se spune în fondurile mutuale sau cele de investiții, performanțele trecute nu sunt un indicator al așteptărilor pentru viitoarele performanțe.