Cum se calculează probabilitățile ruletei (matematic)

În ciuda tuturor discuțiilor despre probabilități și statistici, se pare că puțini oameni pot de fapt calcula matematic șansa unui rezultat la ruletă. Uneori recurg la tabele excel sau folosesc programe specializate, încercând să testeze milioane de rotiri, pentru a obține numărul potrivit. Când cineva înțelege probabilitatea de bază, se poate răspunde la aproape orice întrebare cu privire la certitudinea oricărui rezultat folosind un calculator, sau doar introducând ecuația ca formulă într-un simplu fișier excel.

Mai întâi trebuie să înțelegem care este funcția factorială, simbolizată prin: „!”
Va trebui să înmulțim o serie de numere naturale descendente.
Exemple:
4! = 4 × 3 × 2 × 1 = 24
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
1! = 1
0! = 1 (axiomatic)

La ruletă, în termeni practici, un factorial arată în câte moduri, diferite elemente (sau numere) pot fi aranjate. Fără repetări ale aceluiași articol sau număr. Pentru a vă face o idee asupra acestui total, și cât de mare poate deveni luând în calcul 37 de numere (ruleta europeană):
37! = 1,3763753 × 1043

Aceasta înseamnă că există multe trilioane de trilioane de aranjamente diferite ale celor 37 de numere de ruletă, fără a număra posibilele repetări. Iată în câte moduri diferite (secvențe) pot apărea toate numerele de la ruletă în 37 de rotiri. Puteți citi mai multe despre combinațiile matematice aici.

ECUAȚIA PROBABILITĂȚII

Iată principala formulă matematică pentru calcularea șanselor oricărui rezultat sau eveniment al ruletei.
Mai întâi trebuie să definim parametrii:
P (e) este probabilitatea unui eveniment E.
n este numărul de încercări (rotiri)
x reprezintă numărul de câștiguri al pariului nostru
P (b) este probabilitatea ca pariul (bet) „B” nostru să câștige într-o singură rotire

Probabilitatea P(e) evenimentului E = [Pariul b plasat de x ori în n rotiri] =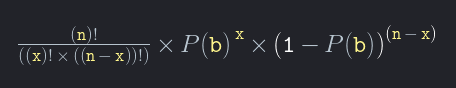

încă o dată:

P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x

Dacă doriți să analizați această ecuație și mai profund, puteți cerceta distribuția binomială, care stă la baza majorității probabilităților de ruletă. De asemenea, vreau să subliniez diferența importantă dintre probabilitate și expectativă. Iată o metodă rapidă și ușoară de a calcula riscul la ruletă, iar acest articol vă va ajuta să înțelegeți și să calculați valoarea așteptată al oricărui pariu.

Acum, să urmărim cât de eficientă este această metodă din punct de vedere practic. Următoarele exemple vă vor ajuta să înțelegeți mai bine cum funcționează formula.

EXEMPLU DE ȘANSE SIMPLE

Să presupunem că vrem să calculăm probabilitatea de a nimeri două diviziuni negre în trei rotiri. Altfel spus: „cât de des vom vedea exact două numere negre în trei rotiri”. Rețineți că această ecuație calculează precis probabilitățile unui eveniment specific. Nu probabilitatea de a nimeri două sau mai multe diviziuni negre, ci exact două.
Parametrii sunt următorii:
n = 3 (rotiri totale)
x = 2 (Numere negre / rotiri câștigătoare)
P (b) = 0,5 (probabilitatea de a nimeri un număr negru / rotire - ignorăm zero pentru simplitate)

P (e) = (n! / (X! (N-x)!)) P (b) x (1-P (b)) n-x
P (e) = (3! / (2! (3-2)!)) 0,52 (1-0,5) 3-2
P (e) = (3! / (2! 1!)) 0,52 0,51
P (e) = (3 × 2 × 1/2 × 1 × 1) 0,25 × 0,5
P (e) = (3/1) 0,25 × 0,5
P (e) = 3 × 0,125 = 0,375

Prin urmare, probabilitatea de a nimeri exact 2 numere negre în 3 rotiri este de 0,375 (ori 37,5%), sau puțin mai mult de 1/3. Toate aceste numere sunt doar expresii diferite ale aceleiași idei.
 

EXEMPLE DUZINĂ

Vrem să calculăm probabilitatea ca o anume secțiune (duzină) de la masă (deci nu o secțiune oarecare) să nimerească exact de 2 ori în 6 rotiri.
n = 6
x = 2
P (b) = 12/37

P (e) = (6! / (2! (6-2)!)) (12/37) 2 (1-12 / 37) 6-2
P (e) = (6 × 5 × 4! / (2! 4!)) 0,3242 0,6764
P (e) = (30/2) 0,105 × 0,209
P (e) = 15 × 0,022
P (e) = 0,329 sau 32,9% sau aproximativ 1/3

EXEMPLU DE NUMĂR UNIC

Știți că în ruleta europeană, probabilitatea ca un anumit număr să apară într-o singură rotire este 1/37 sau 2,7%. Dar care este probabilitatea ca un anumit număr să apară exact 1 dată în 37 de rotiri?

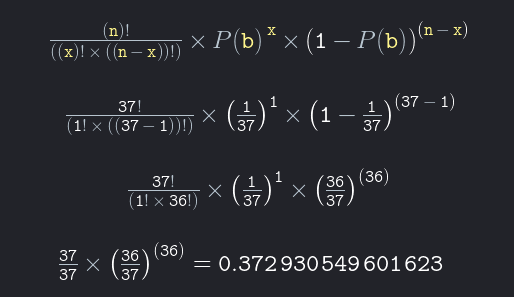
Probabilitatea ca un anumit număr să apară exact 1 dată în cursul a 37 de rotiri este de 0,373 sau 37,3%.

Folosind aceeași formulă, putem calcula probabilitatea ca un anumit număr să nu apară deloc în 37 de rotiri (0,362 sau 36,2%) și probabilitatea ca acesta să apară de două ori (0,186 sau 18,6%).
Formula matematică pe care am prezentat-o adineauri poate fi aplicată pentru a determina orice probabilități de ruletă sub forma „Pariul B care nimerește de X ori în N rotiri”.

UN NUMĂR CARE SE REPETĂ DE 3 ORI ÎN 38 DE ROTIRI LA ROULETA AMERICANĂ

Introducând valorile relevante în ecuația principală obținem: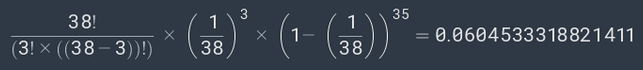

Șansa ca acest lucru să se petreacă este de 0,06 sau 6% sau 1 / 16,6.
În consecință, ne putem aștepta ca un astfel de fenomen să apară o dată la 633 de rotiri. Deoarece după 38 de rotiri probabilitatea este de 1 / 16,6, în medie, calculul ne indică: 38 * 16,6 = 633 de rotiri

Iată un calculator util cu funcția COPY - PASTE unde puteți aplica aceste calcule.

Pentru mai multe informații vizitați Khan Academy.